Creative Prediction with Neural Networks

So are Bio-Signals

Image Credit: Wikimedia

Categorical vs. Continuous Models

Normal (Gaussian) Distribution

Problem: Normal distribution might not fit data

Mixture of Normals

This solves our problem:

Mixture Density Networks

• Idea: output parameters of a mixture model instead!
• Rather than MSE for training, use the PDF of the mixture model.
• Now network can model complicated distributions! 😌

Simple Example in Keras

Difficult data is not hard to find! Think about modelling an inverse sine (arcsine) function.

• input value takes multiple outputs…
• is not going to go well for a single normal model.

MDN Architecture:

Loss function for MDN is negative log of likelihood function \(\mathcal{L}\).

Feedforward MDN Solution

Two-hidden-layer MDN (510 parameters)---code snippet:

N_MIXES = 5
model = Sequential()
model.add(Dense(15, batch_input_shape=(None, 1), activation='relu'))
model.add(Dense(15, activation='relu'))
model.add(mdn.MDN(1, N_MIXES)) # here's the MDN layer!
model.compile(loss=mdn.get_mixture_loss_func(1,N_MIXES), optimizer='rmsprop')
model.summary()

Feedforward MDN Results

Two-hidden-layer MDN (510 parameters)---works much better!

Getting inside the MDN layer

def elu_plus_one_plus_epsilon(x):
    return (K.elu(x) + 1 + 1e-8)

N_HIDDEN = 15; N_MIXES = 5
inputs = Input(shape=(1,), name='inputs')
hidden1 = Dense(N_HIDDEN, activation='relu', name='hidden1')(inputs)
hidden2 = Dense(N_HIDDEN, activation='relu', name='hidden2')(hidden1)
mdn_mus = Dense(N_MIXES, name='mdn_mus')(hidden2)
mdn_sigmas = Dense(N_MIXES, activation=elu_plus_one_plus_epsilon, name='mdn_sigmas')(hidden2)
mdn_pi = Dense(N_MIXES, name='mdn_pi')(hidden2)
mdn_out = Concatenate(name='mdn_outputs')([mdn_mus, mdn_sigmas, mdn_pi])
model = Model(inputs=inputs, outputs=mdn_out)

Loss Function: The Tricky Bit.

Loss function for the MDN should be the negative log likelihood:

def mdn_loss(y_true, y_pred):
    # Split the inputs into paramaters
    out_mu, out_sigma, out_pi = tf.split(y_pred, num_or_size_splits=[N_MIXES, N_MIXES, N_MIXES],
                                         axis=-1, name='mdn_coef_split')
    mus = tf.split(out_mu, num_or_size_splits=N_MIXES, axis=1)
    sigs = tf.split(out_sigma, num_or_size_splits=N_MIXES, axis=1)
    # Construct the mixture models
    cat = tfd.Categorical(logits=out_pi)
    coll = [tfd.MultivariateNormalDiag(loc=loc, scale_diag=scale) for loc, scale
            in zip(mus, sigs)]
    mixture = tfd.Mixture(cat=cat, components=coll)
    # Calculate the loss function
    loss = mixture.log_prob(y_true)
    loss = tf.negative(loss)
    loss = tf.reduce_mean(loss)
    return loss

model.compile(loss=mdn_loss, optimizer='rmsprop')

Let’s go through bit by bit…

Loss Function: Part 1:

First we have to extract the mixture paramaters.

# Split the inputs into paramaters
out_mu, out_sigma, out_pi = tf.split(y_pred, num_or_size_splits=[N_MIXES, N_MIXES, N_MIXES],
                                     axis=-1, name='mdn_coef_split')
mus = tf.split(out_mu, num_or_size_splits=N_MIXES, axis=1)
sigs = tf.split(out_sigma, num_or_size_splits=N_MIXES, axis=1)

• Split up the parameters \(\boldsymbol\mu\), \(\boldsymbol\sigma\), and \(\boldsymbol\pi\), remember that there are N_MIXES \(= K\) of each of these.
• \(\boldsymbol\mu\) and \(\boldsymbol\sigma\) have to be split again so that we can iterate over them (you can’t iterate over an axis of a tensor…)

Loss Function: Part 2:

Now we have to construct the mixture model’s PDF.

# Construct the mixture models
cat = tfd.Categorical(logits=out_pi) 
coll = [tfd.Normal(loc=loc, scale=scale) for loc, scale
        in zip(mus, sigs)]
mixture = tfd.Mixture(cat=cat, components=coll)

• For this, we’re using the Mixture abstraction provided in tensorflow-probability.distributions.
• This takes a categorical (a.k.a. softmax, a.k.a. generalized Bernoulli distribution) model, and a list the component distributions.
• Each normal PDF is contructed using tfd.Normal.
• Can do this from first principles as well, but good to use abstractions that are available (?)

Loss Function: Part 3:

Finally, we calculate the loss:

loss = mixture.log_prob(y_true)
loss = tf.negative(loss)
loss = tf.reduce_mean(loss)

• mixture.log_prob(y_true) means “the log-likelihood of sampling y_true from the distribution called mixture.”

Some more details….

• This “version” of a mixture model works for a mixture of 1D normal distributions.
• Not too hard to extend to multivariate normal distributions, which are useful for lots of problems.
• This is how it actually works in my Keras MDN layer, have a look at the code for more details…

MDN-RNNs

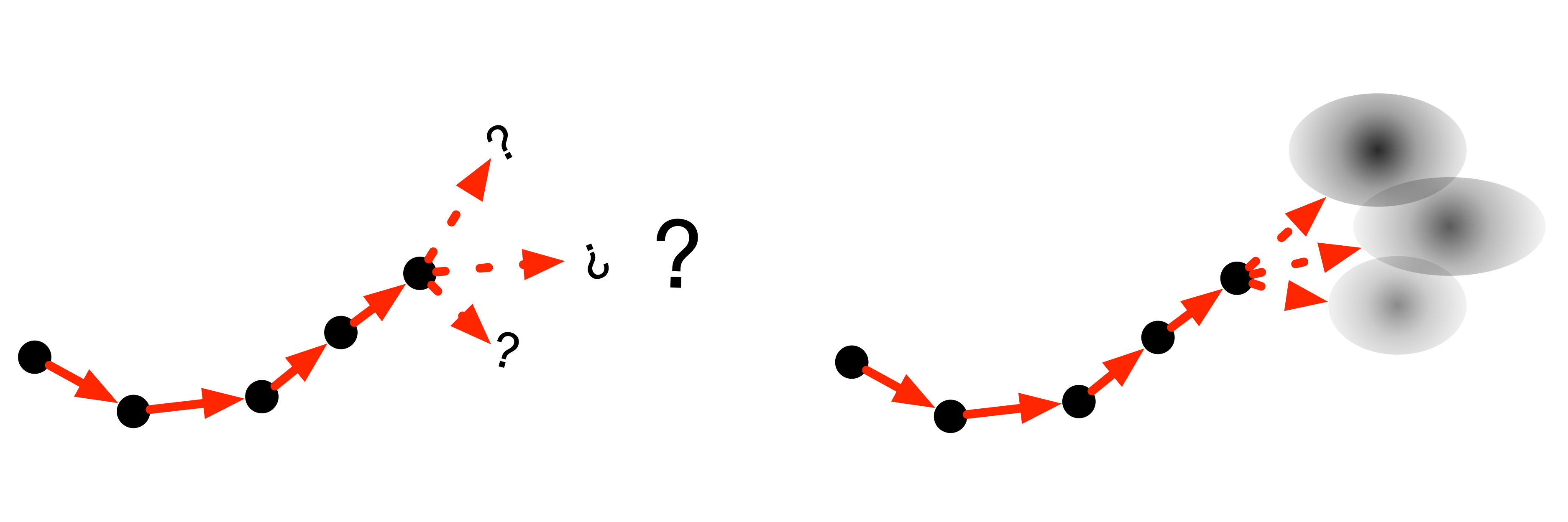
MDNs can be handy at the end of an RNN! Imagine a robot calculating moves forward through space, it might have to choose from a number of valid positions, each of which could be modelled by a 2D Normal model.

MDN-RNN Architecture

Can be as simple as putting an MDN layer after recurrent layers!

Use Cases: Handwriting Generation

• Handwriting Generation RNN (Graves, 2013).
• Trained on handwriting data.
• Predicts the next location of the pen (\(dx\), \(dy\), and up/down)
• Network takes text to write as an extra input, RNN learns to decide what character to write next.

Use Cases: SketchRNN

• SketchRNN Kanji (Ha, 2015); similar to handwriting generation, trained on kanji and then generates new “fake” characters
• SketchRNN VAE (Ha et al., 2017); similar again, but trained on human-sourced sketches. VAE architecture with bidirectional RNN encoder and MDN in the decoder part.

Use Cases: RoboJam

Use Cases: World Models

• World Models (Ha & Schmidhuber, 2018)
• Train a VAE for visual perception an environment (e.g., VizDoom), now each frame from the environment can be represented by a vector \(z\)
• Train MDN to predict next \(z\), use this to help train an agent to operate in the environment.

References

1. Christopher M. Bishop. 1994. Mixture Density Networks. Technical Report NCRG/94/004. Neural Computing Research Group, Aston University.
2. Axel Brando. 2017. Mixture Density Networks (MDN) for distribution and uncertainty estimation. Master’s thesis. Universitat Politècnica de Catalunya.
3. A. Graves. 2013. Generating Sequences With Recurrent Neural Networks. ArXiv e-prints (Aug. 2013). ArXiv:1308.0850
4. David Ha and Douglas Eck. 2017. A Neural Representation of Sketch Drawings. ArXiv e-prints (April 2017). ArXiv:1704.03477
5. Charles P. Martin and Jim Torresen. 2018. RoboJam: A Musical Mixture Density Network for Collaborative Touchscreen Interaction. In Evolutionary and Biologically Inspired Music, Sound, Art and Design: EvoMUSART ’18, A. Liapis et al. (Ed.). Lecture Notes in Computer Science, Vol. 10783. Springer International Publishing. DOI:10.1007/9778-3-319-77583-8_11
6. D. Ha and J. Schmidhuber. 2018. Recurrent World Models Facilitate Policy Evolution. ArXiv e-prints (Sept. 2018). ArXiv:1809.01999