Creative Prediction with Neural Networks
A course in ML/AI for creative expression
Deep Dive on RNNs
Charles Martin - The Australian National University
Ngunnawal & Ngambri & Ngarigu Country
What is an Artificial Neuron?
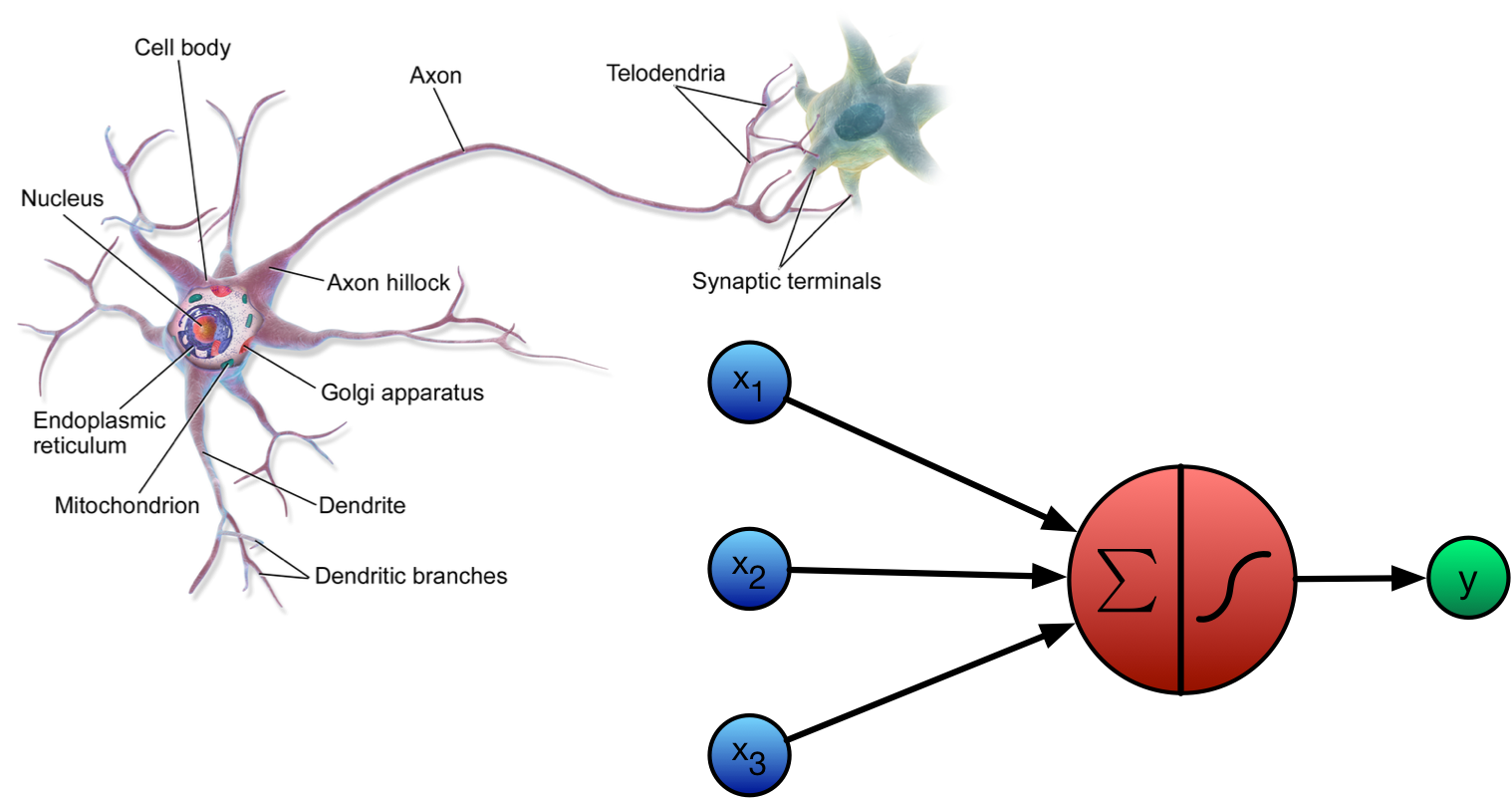
Feed-Forward Network

For each unit: \(y = \text{tanh}\big(Wx + b \big)\)
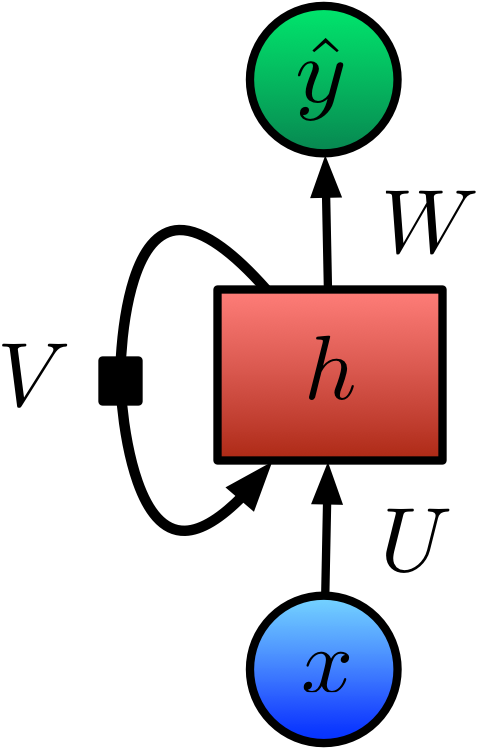
Recurrent Network

For each unit: \(y_t = \text{tanh}\big(Ux_t + Vh_{t-1} + b \big)\)
Sequence Learning Tasks



Recurrent Network

simplifying…
Recurrent Network
simplifying and rotating…
“State” in Recurrent Networks

- Recurrent Networks are all about storing a “state” in between computations…
- A “lossy summary of… past sequences”
- h is the “hidden state” of our RNN
- What influences h?
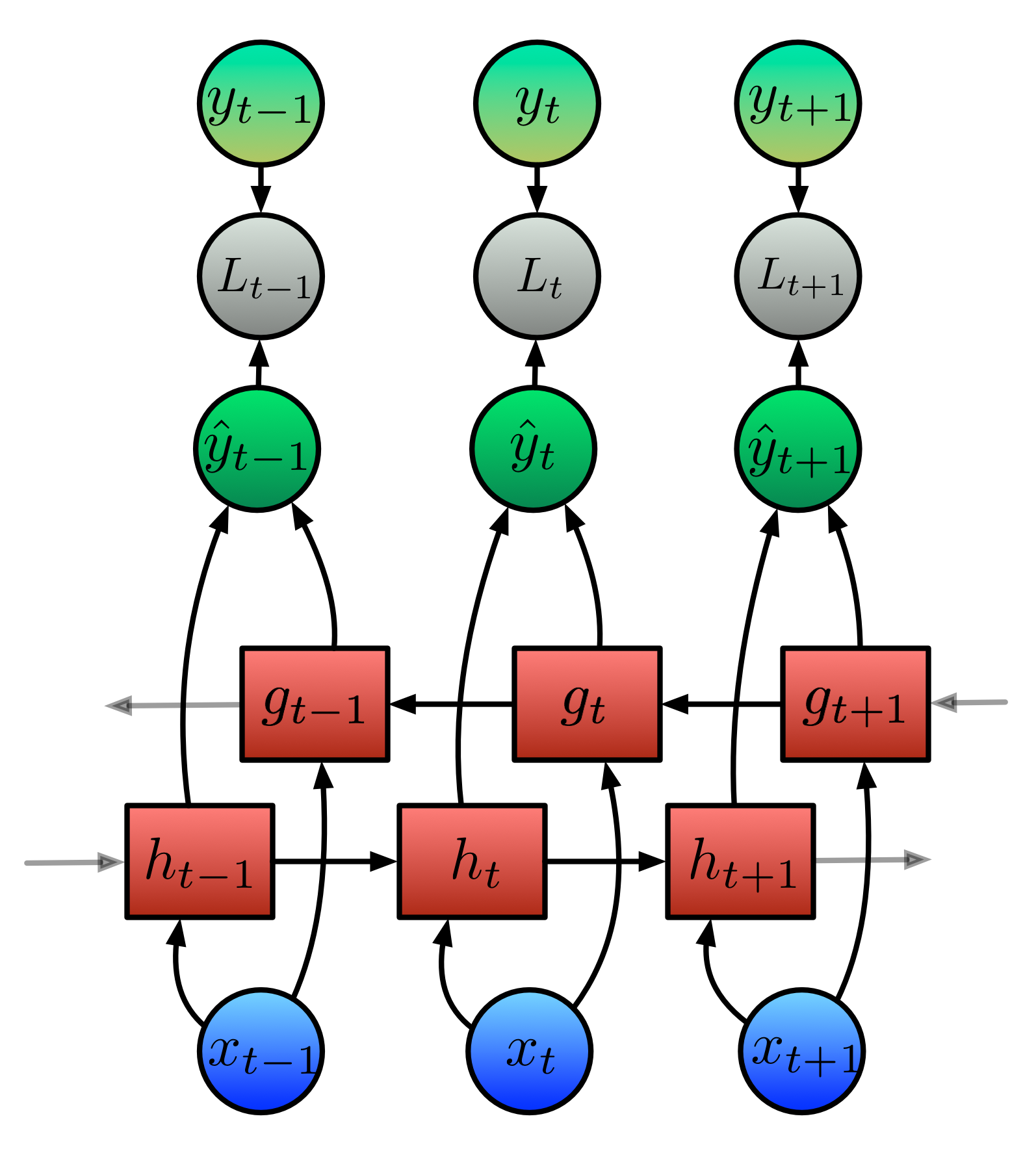
Defining the RNN State

We can define a simplified RNN represented by this diagram as follows:
\[h_t = \text{tanh}\big(Ux_t + Vh_{t-1} + b \big)\]
\[\hat{y}_t = \text{softmax}(c + Wh_t)\]
Unfolding an RNN in Time
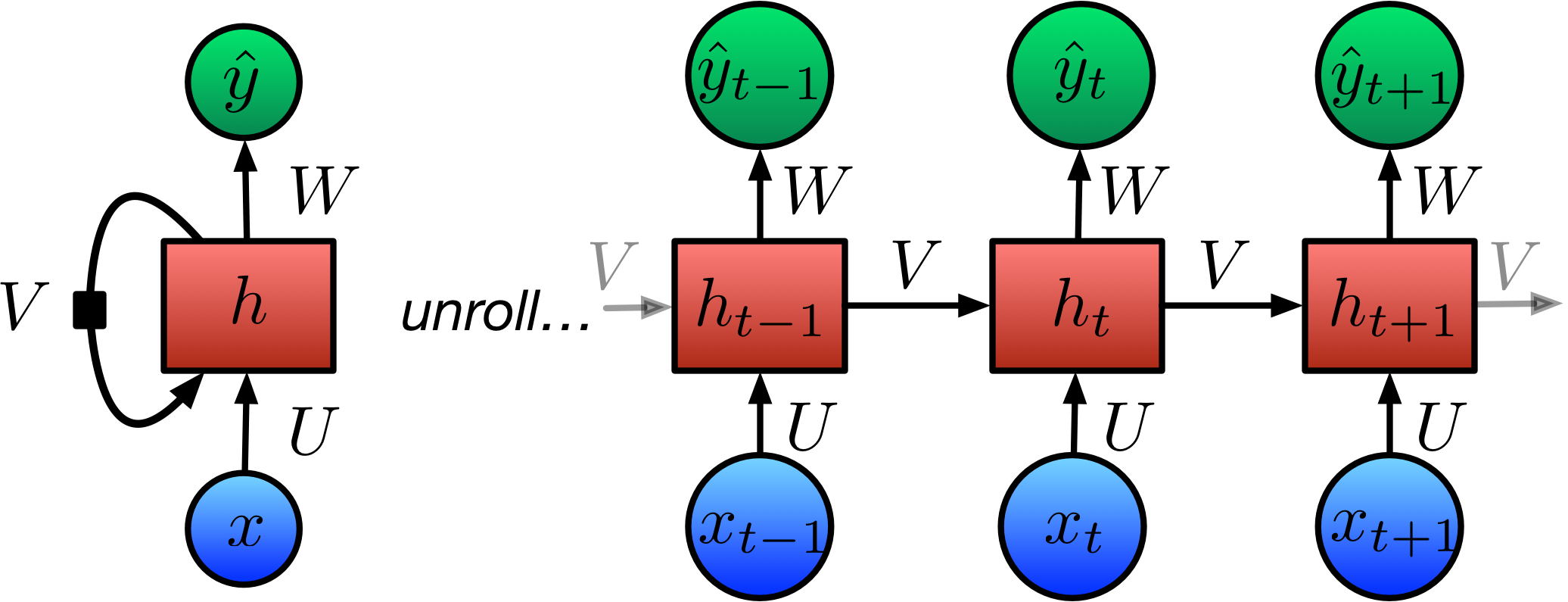
- By unfolding the RNN we can compute \(\hat{y}\) for a given length of sequence.
- Note that the weight matrices \(U\), \(V\), \(W\) are the same for each timestep; this is the big advantage of RNNs!
Forward Propagation

We can now use the following equations to compute \(\hat{y}_t\), by computing \(h\) for the previous steps:
\[h_t = \text{tanh}\big(Ux_t + Vh_{t-1} + b \big)\]
\[\hat{y}_t = \text{softmax}(c + Wh_t)\]
Y-hat is Softmax’d

\(\hat{y}\) is a probability distribution!
\[\sigma(\mathbf{z})_j = \frac{e^{z_j}}{\sum_{k=1}^K e^{z_k}} \text{ for } j = 1,\ldots, K\]
Calculating Loss: Categorical Cross Entropy
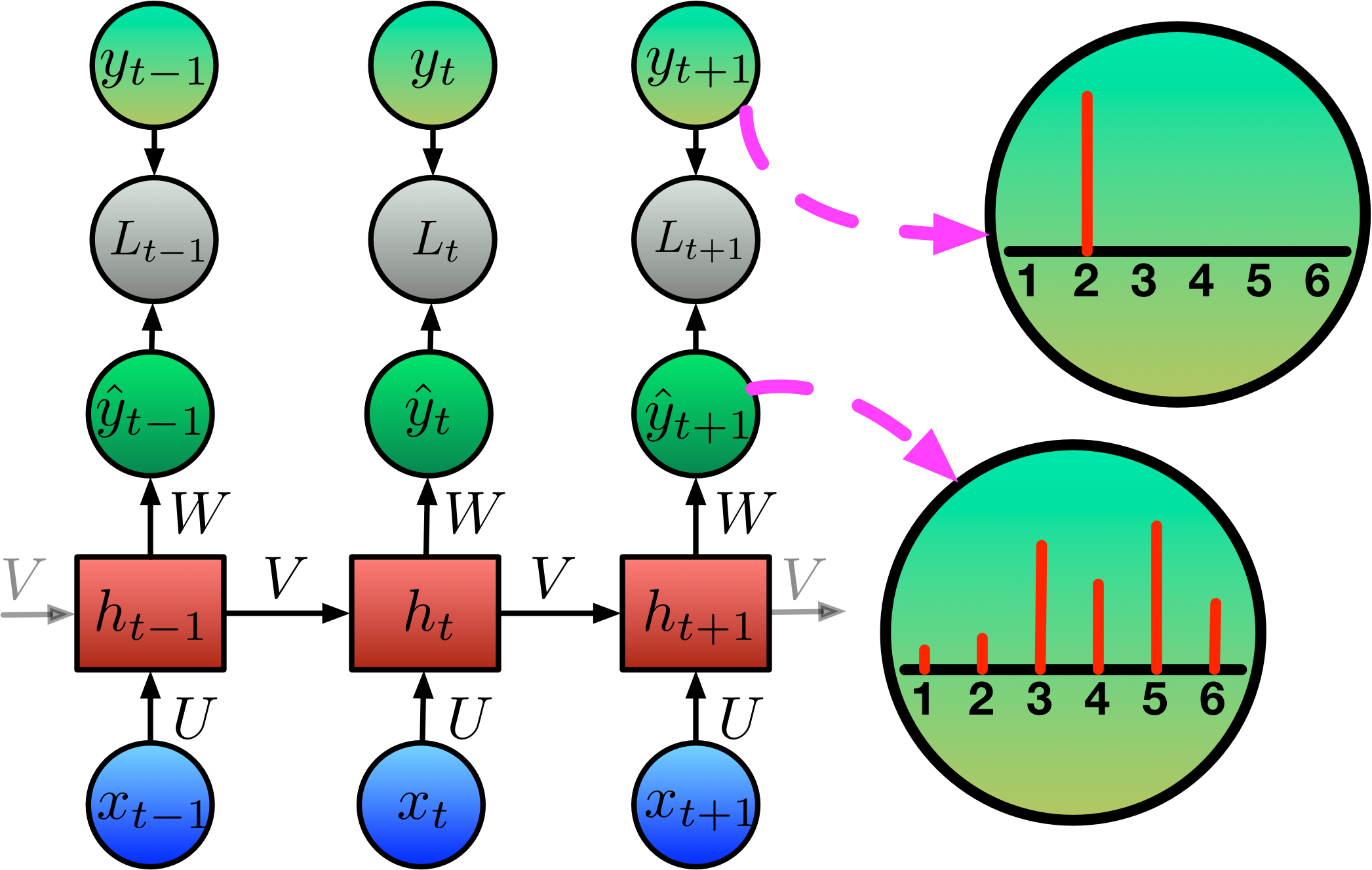
We use the categorical cross-entropy function for loss:
\[\begin{align*} h_t &= \text{tanh}\big( {b} + {Vh}_{t-1} + {Ux}_t \big) \\ \hat{y}_t &= \text{softmax}(c + Wh_t) \\ L_t &= -y_t \cdot \text{log}(\hat{y}_t) \\ \text{Loss} &= \sum_t L_t \\ \end{align*}\]
Backpropagation Through Time (BPTT)

Propagates error correction backwards through the network graph, adjusting all parameters (U, V, W) to minimise loss.
Example: Character-level text model
- Training data: a collection of text.
- Input (X): snippets of 30 characters from the collection.
- Target output (y): 1 character, the next one after the 30 in each X.
Training the Character-level Model

- Target: A probability distribution with \(P(n) = 1\)
- Output: A probability distribution over all next letters.
- E.g.: “My cat is named Simon” would lead to X: “My cat is named Simo” and y: “n”
Using the trained model to generate text

- S: Sampling function, sample a letter using the output probability distribution.
- The generated letter is reinserted at as the next input.
- We don’t want to always draw the most likely character. The would give frequent repetition and “copying” from the training text. Need a sampling strategy.
Char-RNN
- RNN as a sequence generator
- Input is current symbol, output is next predicted symbol.
- Connect output to input and continue!
- CharRNN simply applies this to a (subset) of ASCII characters.
- Train and generate on any text corpus: Fun!
Char-RNN Examples
Shakespeare (Karpathy, 2015):
Second Senator: They are away this miseries, produced upon my soul, Breaking and strongly should be buried, when I perish The earth and thoughts of many states.
DUKE VINCENTIO: Well, your wit is in the care of side and that.
Latex Algebraic Geometry:

N.B. “Proof. Omitted.” Lol.
Time to Hack
Making an RNN that generates Star Trek titles
RNN Architectures and LSTM
Bidirectional RNNs
- Useful for tasks where the whole sequence is available.
- Each output unit (\(\hat{y}\)) depends on both past and future - but most sensitive to closer times.
- Popular in speech recognition, translation etc.
Encoder-Decoder (seq-to-seq)

Learns to generate output sequence (y) from an input sequence (x).
Final hidden state of encoder is used to compute a context variable C.
For example, translation.
Deep RNNs

- Does adding deeper layers to an RNN make it work better?
- Several options for architecture.
- Simply stacking RNN layers is very popular; shown to work better by Graves et al. (2013)
- Intuitively: layers might learn some hierarchical knowledge automatically.
- Typical setup: up to three recurrent layers.
Long-Term Dependencies
- Big mathematical challenge!
- Gradients propagated through the same weights tend to vanish (mostly) or explode (rarely)
- E.g., consider an RNN with no nonlinear activation function or input.
- Each time step multiplies h(0) by W.
- This corresponds to raising power of eigenvalues in \(\Lambda\).
- Eventually, components of h(0) not aligned with the largest eigenvector will be discarded.
\[\begin{align*} h_t &= Wh_{t-1}\\ h_t &= (W^t)h_0 \end{align*}\]
(supposing W admits eigendecomposition with orthogonal matrix Q)
\[\begin{align*} W &= Q\Lambda Q^{\top}\\ h_t &= Q\Lambda ^t Qh_0 \end{align*}\]
Gated RNNs

- Provide gates that can change the hidden state a little bit at each step.
- The gates are controlled by learnable weights as well!
- Hidden state weights that may change at each time step.
- Create paths through time with derivatives that do not vanish/explode.
- Gates choose information to accumulate or forget at each step.
Long Short-Term Memory
- Self-loop containing internal state (c).
- Three extra gating units:
- Forget gate: controls how much memory is preserved.
- Input gate: control how much of current input is stored.
- Output gate: control how much of state is shown to output.
- Each gate has own weights and biases, so this uses lots more parameters.

Other Gating Units
 Source: (Olah, C. 2015.)
Source: (Olah, C. 2015.)
- Are three gates necessary?
- Other gating units are simpler, e.g., Gated Recurrent Unit (GRU)
- For the moment, LSTMs are winning in practical use.
- Alternative unit design: project idea?
Visualising LSTM activations
Sometimes, the LSTM cell state corresponds with features of the sequential data:

Source: (Karpathy, 2015)
CharRNN Applications: FolkRNN
Some kinds of music can be represented in a text-like manner.

Other CharRNN Applications
Google Magenta Performance RNN


- State-of-the-art in music generating RNNs.
- Encode MIDI musical sequences as categorical data.
- Now supports polyphony (multiple notes), dynamics (volume), expressive timing (rubato).
- E.g.: YouTube demo
Neural iPad Band, another CharRNN


- iPad music transcribed as sequence of numbers for each performer.
- Trick: encode multiple ints as one (preserving ordering).
- Video
Time to Hack
These examples run in Google Colaboratory, just click the link to start them up.
Star Trek RNN (open in Colab)
Advanced CharRNN (open in Colab)
Melody Generation (open in Colab)
Books and Learning References
Ian Goodfellow, Yoshua Bengio, and Aaron Courville. 2016. Deep Learning. MIT Press.
François Chollet. 2018. Manning.
Chris Olah. 2015. Understanding LSTMs
Karpathy. 2015. The Unreasonable Effectiveness of RNNs
Foster. 2019. Generative Deep Learning: Teaching Machines to Paint, Write, Compose, and Play


